Academics
At Albion, you’ll get to do a little bit of everything and a lot of what you love. Our liberal arts curriculum allows you to explore your academic options while you grow as a critical thinker and communicator, skills that will serve you well in any career. You’ll pursue your passions and learn to translate ideas into action. And you’ll do it in a supportive environment where you belong, surrounded by faculty and peers all committed to one another’s success.

Majors and Programs
We offer nearly 90 areas of study in the humanities, social sciences, fine and performing arts, business and economics and law and policy.
Whichever path of study you choose, you’ll benefit from small classes, close faculty mentorship and plenty of opportunities for active learning.
Explore Majors & Programs
Centers and Institutes
For students who want to make an immediate impact in their chosen field of study, Albion’s renowned centers and institutes are designed to provide firsthand experiences, support, and networking resources to accelerate futures in the areas of public policy, medicine, race and belonging, sustainability, teacher development, business, and management.
Explore Centers & InstitutesFirst-Year Experience

We want Albion to feel like you belong right away. We created our First-Year Experience (FYE) program to provide you with both academic and social support as you transition from high school to college. The program includes peer mentorship, seminars, learning strategies sessions and more.
Student Research
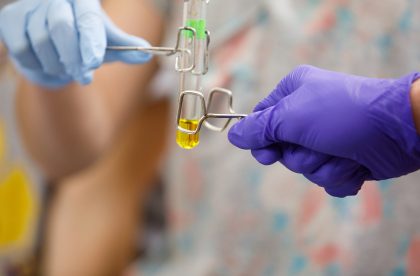
You’ll get to know your professors well in the classroom, but you’ll also have opportunities to get to know them as mentors and partners. Work alongside faculty on their research and yours, as early as your first year at Albion.
Study Away

The Albion classroom spans the country and the globe. Make your education a bit of an adventure. Spend a summer or a semester interning at a New York City museum, studying sustainable development in Costa Rica, or doing a full language immersion program in France.
Honors Program

In our Prentiss M. Brown Honors Program, you’ll study science, humanities, fine arts and social sciences. You’ll have access to a number of challenging and rewarding experiences, culminating in a senior thesis. Honors Program graduates have won National Science Foundation research awards, Udall Foundation awards and a number of Fulbright fellowships.
Student Resources
Find important information and explore the resources and support services available to you as an Albion student.